Class notes for 1/28

More on frequency tables: When we have a lot of duplicate values in a data set, a frequency table lets us write that data more compactly, by listing each value x, followed by the positive number of times it shows up, f(x). Let's look at the data list from the 1/26 notes, which were the scores in one of the two classes this semester on the first quiz.

x || f(x)

20 || 2
19 || 1
18 || 2
17 || 5
16 || 7
15 || 2
14 || 5
13 || 5
12 || 3
11 || 5
_9 || 2
_8 || 1
_7 || 2
_4 || 3


We already discussed how to find the mode and median, but what about the mean? We need to find n, and we need to find the sum of all the x values. To get those numbers, n = sum(f(x)) and sum(x) = sum(x*f(x)). Here is the list again with another column of numbers added, the value multiplied by its frequency.

x || f(x) || x*f(x)

20 || 2 || 40
19 || 1 || 19
18 || 2 || 36
17 || 5 || 85
16 || 7 ||112
15 || 2 || 30
14 || 5 || 70
13 || 5 || 65
12 || 3 || 36
11 || 5 || 55
_9 || 2 || 18
_8 || 1 || _8
_7 || 2 || 14
_4 || 3 || 12

The sum of the second column is 45, the sum of the third column is 600, so x-bar=600/45=13.333..., or rounded to the nearest tenth, 13.3.


The ideas of John Tukey. John Tukey was a statistician and computer scientist who did a lot of his best work back in the 1960s. Many of his ideas in statistics are about easier and shorter ways to present data sets. We will study three of them, the stem and leaf plot, the five number summary and its graphical representation, the box and whiskers plot.

Stem and leaf plots. If we don't have a lot of duplication, a frequency table is not going to make presenting data any shorter. What Tukey did was split numbers into two parts, the stem and the leaf. The standard way to do this is to make the last digit the leaf and the rest of the number the stem. For example, the number 87 would have stem = 8 and leaf = 7. Tukey's idea was to put the stem numbers at the left and list the leaves from low to high, using a mono-spaced font, which back in the day of typewriters was the only choice available for someone typing. (Courier is a mono-spaced font. The letter i is the same width as the letter w or any other symbol. Most fonts used today aren't mono-spaced anymore, but in this situation, we want to use Courier.)

Here is a list of numbers. It is the number of wins by teams in the American League at the end of the 2008 regular season.

97, 95, 89, 86, 68, 89, 88, 81, 75, 74, 100, 79, 75, 61

The highest number is 100, so we make the stem 10 and the leaf 0. All the numbers on the list are put in stem and leaf form, where the stem is underlined and followed by a |, then the leaves are listed from low to high from left to right.

____
10 | 0
_9 | 57
_8 | 16899
_7 | 4559
_6 | 18

Sometimes data is too spread out to use the last digit as the leaf, and instead the last two digits are the leaf, and we put a space between the two digit leaves for readability. Here is an example. This data set is the number of points scored by the teams in the AFC in the 2008 regular season.

Data set: 347, 448, 388, 440, 234, 298, 394, 367, 223, 244, 364, 350, 342, 356, 309, 317

44 | 08
43 |
42 |
41 |
40 |
39 | 4
38 | 8
37 |
36 | 47
35 | 06
34 | 27
33 |
32 |
31 | 7
30 | 9
29 | 8
28 |
27 |
26 |
25 |
24 | 4
23 | 4
22 | 3

If each stem is a span of ten values, this data is too spread out, but if the stems go from 200 to 299, 300 to 399 and 400-499, the stem and leaf method works very well. When the leaves are two digits, we put a space between them for easier reading.

___
4 | 40 48
3 | 09 17 42 47 50 56 64 67 88 94
2 | 23 34 44 98

Now the data is in a more compact list, and the big idea of stem and leaf, which is not only to give the values but to give the shape of the data, becomes clear. There are only a few values in the 400-499 range, most are between 300 and 399, with some low values in the 200s.

It's possible to have the opposite problem where a stem has too many leaves. Here is the stem and leaf version of the data set we represented with a frequency table earlier.

___
2 | 00
1 | 11111222333334444455666666677777889
0 | 44477899

Obviously, the vast majority of the data is between 10 and 19. It makes sense to make more stems by splitting each category in half, going from 0 to 4, 5 t0 9, 10 to 14, 15 to 19 and 20 to 24. Since there is no data above 25, we don't have to create an empty stem from 25 to 29.


___
2 | 00
1 | 55666666677777889
1 | 111112223333344444
0 | 77899
0 | 444

This shows us that the most common values were between 10 and 14, with 15 to 19 almost as common, with the frequency trailing off as values get above 19 or under 10.


Five number summary. Both frequency tables and stem and leaf plots tell us about all the data. The five number summary, yet another idea of John Tukey, gives us an idea of how the data is distributed, but leaves a lot of information out. The five numbers are the highest value, the lowest value, and three intermediate numbers, Q1, Q2 and Q3. Q stands for quartile, so these numbers are respectively the cut-off points for the bottom 25% of the data, the bottom 50% of the data and the bottom 75% of the data. We already know Q2 by another name, the median. Once we remove the median from a set of data, we then have two new subsets, the bottom half and the top half. Q1 is the median of the bottom half, while Q3 is the median of the top. Let's do an example with a set of data we have already dealt with, the points scored by AFC teams. First, here is the list of 16 numbers put in order from high to low. The middle two values are marked in bold type.

448, 440, 394, 388, 367, 364, 356, 350, 347, 342, 317, 309, 298, 244, 234 223

The median, or Q2 is (350+347)/2 = 348.5.

Top half: 448, 440, 394, 388, 367, 364, 356, 350

The median of the top half, or Q3 is (388+367)/2 = 377.5.

Bottom half: 347, 342, 317, 309, 298, 244, 234 223

The median of the bottom half, or Q1 is (309+298)/2 = 303.5.

In order, the five number summary is:

High: 448
Q3: 377.5
Q2: 348.5
Q1: 303.5
Low: 223

Box and whisker plots: The box and whisker plot is a graphical representation of the five number summary. Each of the five points is plotted against a number line for scale. The area between and is the box, and it represents the middle 50% of the data. The whiskers are lines from the edge of the box to the high and low values. is shown by a dotted line somewher inside the box, though not exactly in the middle, necessarily.

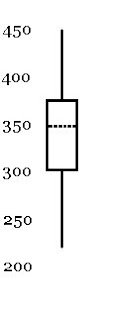
Here is a representation of five number summary above as a box and whisker plot. It could either be on a vertical scale, as pictured here, or it could be represented on a horizontal scale. When financial data from a set of time periods is summarized, the data is often represented with box and whiskers plots, though some websites call them candlesticks instead. The vertical scale represents the value in currency (usually dollars), while the horizontal scale represents the change in time, where the time periods can be any standardized amount, whether day to day or week to week or month to month.

Inputting a data set into the TI-30X II s

In the following instructions, I will write comments in this font and the stuff from the calculator in a blocky font called Courier. The things the calculator will put on the screen are in black, while the keys you type in will be in red.

First, you want to be in one-variable stat mode. If you are in stat mode, the word STAT shows up on the output screen in small letters.

Step 0: If you don't see the word STAT on your screen, type the following.

[2nd][DATA][ENTER]

This puts you in stat mode. Before you hit enter, the screen should read

1-VAR 2-VAR

and by pressing enter when 1-VAR is underlined, you go into 1-variable statistics mode. You can skip now to Step 2.

Step 1: If you see the word STAT on the screen, type the following.

[2nd][DATA]

What you will see are the words

1-VAR 2-VAR [left][left]

come up on the screen, and then when you scroll left twice, you will see the word

CLRDATA [ENTER]

underlined. That's when you press enter, which clears out any old data you have.

Step 2: Inputting a data set. The two important buttons here are [DATA] and [STATVAR]. [DATA] lets you start inputting data, and when you are finished pressing [STATVAR] will get you to the statistics associated with the data set you just entered.

One variable statistics in the TI-30X II s are input as a frequency table, a value followed by how many times it shows up on the list. Consider the following list.

20, 20, 19, 18, 18, 17, 17, 17, 17, 17, 16, 16, 16, 16, 16, 16, 16, 15, 15,
14, 14, 14, 14, 14, 13, 13, 13, 13, 13, 12, 12, 12, 11, 11, 11, 11, 11,
9, 9, 8, 7, 7, 4, 4, 4,

[DATA]
x1= 20 [down]
frq= 2 [down]
x2= 19 [down]
frq= 1 [down]
x3= 18 [down]
frq= 2 [down]
x4= 17 [down]
frq= 5 [down]
x5= 16 [down]
frq= 7 [down]
x6= 15 [down]
frq= 2 [down]
x7= 14 [down]
frq= 5 [down]
x8= 13 [down]
frq= 5 [down]
x9= 12 [down]
frq= 3 [down]
x10= 11 [down]
frq= 5 [down]
x11= 9 [down]
frq= 2 [down]
x12= 8 [down]
frq= 1 [down]
x13= 7 [down]
frq= 2 [down]
x14= 4 [down]
frq= 3 [down]
x15= [STATVAR]

The screen will go blank, then show the word CALC for a few seconds, then the statistics for the data set appear. You can use the [left] and [right] buttons to look at different statistics. The number that appears is the underlined statistic. On this list, the numbers are as follows.

Step 3: Reading the statistics of the sample. (Or it could be the parameters of the population, depending on how the data set was defined.)

What you will see on the screen is in black, what keys you will press are in red. The only key in these instructions are the left button, but the right button works for scrolling as well.

n x-bar sx sigmax
45 [left]
n x-bar sx sigmax
13.333333... [left]
n x-bar sx sigmax4.073193967 [left]n x-bar sx sigmax
4.027681991 [left]
sum(x) sum(x^2)
600 [left]
sum(x) sum(x^2)
8730

To get out of the screen showing the statistics, press [CLEAR]. If you press [ENTER] instead, the screen will show the equation line with the symbol of the statistic you were looking at added to whatever equation you were just looking at. This will be useful later in the class when we need the average x-bar and one of the standard deviations, either sx or sigmax, for calculating z-scores.

If you have any questions about how to use one-variable mode on the TI-30 X II s, leave a comment or send me an e-mail.

Class notes for 1/26

In earlier classes, we discussed three measures of center.

Mean (average)
Type of data: numerical
Method: add up all the numbers and divide by n (or N), the number of things on the list.

Median
Type of data: numerical or ordered categorical
Method: Put the values in order and find the "middle value" which is the value in position (n+1)/2. If n is odd, there is a single median value on the list. If n is even, there are two middle values on the list, and if numerical, take the average of the two. If the data is categorical and the two values aren't the same, the median lies between two categories.

Mode
Type of data: any data can be used, but only if there are duplicate values on the list.
Method: Find the most common value. If there is a tie for most common, there can be more than one mode.

A fourth measure of center was introduced, the mid-range.

Mid-range
Type of data: numerical
Method: (high + low)/2

Sensitivity to outliers: Mid-range is especially sensitive to outlying values, which means values much higher than the rest of the data or much lower than most of the data. Mean is also sensitive, but not as sensitive. Median and mode are not sensitive to outliers at all.

When we should and shouldn't use average: Some types of numerical data do not give useful information when we take the average.

Coded numerical: Usually, with numbers there is a meaning we can give to the ideas of "more" and "less". With coded data, we don't necessarily have that. Examples are zip codes, social security numbers and driver's licenses. Finding the average zip code of a group of people is meaningless, though finding the mode means that is the most popular of the possible zip codes.

Ordinal data: Here, the idea of a > b has meaning, but the distance between units isn't the same. In a ranking system, it's better to be first than it is to be second, but we can't say how much better, and we don't know if the difference between first and second is the same as the distance between second and third.

Often, when we switch from an ordered categorical system like grades (A, B, C, D, F) to the numbers used for grade points (4.0, 3.0, 2.0, 1.0, 0.0), the choice of what numbers to use is arbitrary. Is the distance from an A to B really the same as the distance from a C to a D? Is getting an A in one class and a C in another really the same as getting two Bs, since both would be a 3.0 Grade Point Average (GPA). How about 2 As and a D, which is 3.0, or 3 As and an F? Should all those situations be counted the same way?

Interval data: This is the minimum requirement need for mean to make sense, the idea that the distance between two numbers, a - b, has a consistent meaning, like degrees in temperature readings or the number of strokes taken to complete a round of golf. In these system, the number zero does not mean the complete absence of a thing, so it dividing one number by another from the data set doesn't give meaningful information, but taking and average is about adding values together and dividing by the number of values, so an average temperature or an average of the scores in four rounds of golf does produce a useful statistic.

Rational data: This is data where not only a - b means something, but also a/b. The difference between interval and rational data is the meaning of the number zero. If zero indicates the complete lack of a thing, then we can talk about something between twice as much as another thing, or 10% less. A lot of numerical systems of measurement are rational, but not all.

===

Frequency tables

When we have a lot of repetition in a set of data, a way to write the information more compactly is a frequency table, where a value (either categorical or numerical) is followed by the number of times it shows up in a data set. Here is an example, where we will call the values x and their frequencies f(x).

x || f(x)

20 || 2
19 || 1
18 || 2
17 || 5
16 || 7
15 || 2
14 || 5
13 || 5
12 || 3
11 || 5
_9 || 2
_8 || 1
_7 || 2
_4 || 3

Because there is so much duplication this is much easier to read than 20, 20, 19, 18, 18, 17, 17, 17, 17, 17, etc.

Finding the mode: Whichever value corresponds to the highest frequency is the mode. (Data with no mode would have all frequencies equal to 1, and it would not be a good candidate for being representing as a frequency table.) In the example above, the value 16 shows up seven times, more than any other, so it clearly is the mode.

Finding the median: If we add up all the frequencies, we get n. We need to find (n+1)/2, and figure out which value is in that position. In the data above, n = 45, so the thing in position 23 is the median. We can put the positions of all the data on the list as follows.


x || f(x)

20 || 2 positions 1-2
19 || 1 position 3
18 || 2 positions 4-5
17 || 5 positions 6-10
16 || 7 positions 11-17
15 || 2 positions 18-19
14 || 5 positions 20-24
13 || 5
12 || 3
11 || 5
_9 || 2
_8 || 1
_7 || 2
_4 || 3

This means position 23 is in the middle of a string of values = 14, and 14 is the median.

Next class, we will show how to get an average using a frequency table.

The basics of the TI-30X II S

The TI-30X II S is the recommended calculator for the class. It has many features that will do some very difficult calculations automatically. In the instructions, any time a key press or series of key presses is discussed, the instructions will be in red in the font called Courier.

One of the most important keys on the calculator is the blue key [2nd] at the upper left. Using this key, almost all the black keys and the bottom row of the white keys have double uses. For example, the

[ON]

button is at the lower left. If you press

[2nd][ON]

that turns the calculator off. Some, but not all the functions on the regular black buttons have an inverse function associated with it by pressing 2nd. For example, the 4th button from the bottom in the left column, with [x^2] on it, will square a number, while if you key in [2nd][x^2], it takes the square root of a number. Be careful. To get a square root, you need to type

[2nd][x^2] 3 [ENTER]

which will give you 1.732050808, while to get 3 squared, you type

3 [x^2][ENTER]

to get 9.

To enter in data sets, we will be using the DATA and STATVAR keys, as well as the four arrow buttons in the upper right. Since the four symbols are not available in the text editor I use for this blog, I shall type [up], [down], [left] and [right] to identify the four buttons.

Getting in and out of STAT mode: There are some words written in a small font below the output line for answers. If you see STAT written on that line, this means the calculator has a current set of data it is storing. If you don't see that word, there is nothing currently stored.

If you don't see STAT: Press

[2nd][DATA]

and the equation line of the output screen will give the choices of 1-VAR and 2-VAR. You can use the [left] and [right] buttons to toggle back and forth. Pick the one you want, then press

[ENTER]

(The first data sets we are going to deal with will be 1-variable applications.)

If you want to start a new data set, press

[2nd][DATA][left]

This gives you the CLRDATA option. If you press

[ENTER]

all data that was stored will be erased.

Now we know how to get in and out of STAT mode and erase old data. Next we will learn how to enter a data set and how to get the parameters or statistics, which is to say some of the important numbers associated with the data set, which could be a population or a sample.

Text editor workarounds

Using word processors that don't include some symbols and modes

When writing on the board or using a text editor like Microsoft Word that has a built-in mode for equations, it's easy to write Greek letters or special symbols associated with letters or superscripts or subscripts. Some word processors, like the one used here on the blog or most of the ones that are used to write e-mails, don't have ways to produce these symbols, so there are standard ways to work around these limitations.

Special additions to letters: The symbol for average of a sample is an x with a bar over it. It's pronounced x-bar, and that's the way it is typed if the word processor can't easily put a bar over a letter. We will have a similar situation with a symbol we can type as p-hat, which is the lowercase letter p with a symbol above it that looks like a roof or a hat.

Superscripts: If we need to write "x squared" but can't produce a superscript to make the 2 small and with its base above the line, the standard is to type is "x^2". The up arrow is called a caret, pronounced like carrot, and on your computer keyboard is the shift key and "6" typed together. The caret is also on most TI calculators, and it's the way to perform exponentiation.

Subscripts: We use subscripts to identify particular subjects and their associated values. In the text editor for this blog, it's possible to change font size, so x3 can be written to look like a subscript simply by making the 3 smaller. In text editors where that isn't possible, like most editors used to send e-mail, that would be written as "x_3", where the under bar is the dash "-" and shift typed together.

Greek letters: There are two important symbols in statistics that are lower case letters in the Greek alphabet. If your word processor cannot type these Greek letters, you can use the words "mu" and "sigma". Both of them often have subscripts, so they are typed "mu_x" or "sigma_p", depending on what statistic they are associated with.

Class notes for 1/21

Parameters and statistics. Any number associated with a population is a parameter. Any number associated with a sample is a statistic. It's easy to remember because the associated words begin with the same letter. Methods for remembering things are called mnemonics, pronounced with the leading m silent, named for Mneme, the Greek goddess of memory. The first parameter we learned about is the size of the population, which is always represented with N. The first statistic is the size of the sample, represented by the lowercase letter n.

Subscripts. In general math problems, the letters x and y are often used as variable names. Any letter can be used, and sometimes letters from other languages, most notably Greek are used, especially in trigonometry. When a variable represents a quantity in the world, it makes sense mnemonically to use the letter the word begins with. For instance, if we want to represent the height of a flagpole, the letter h could be used. What if the problem has a second object whose height needs to be measured? Maybe we could call that second height a letter near to h in the alphabet, like g or i or j. What if there are three or four or even more things whose heights have to be kept track of? This is a situation where subscripts become handy.

We could call the height of the first thing h1, the second height h2, the third h3 and so on. We pronounce these names "h one", "h two", "h three", etc. and because there are infinitely many positive whole numbers, we don't have to worry about running out. If you have to write this in a text editor that does not let you make subscripts, the standard is to use an underscore, such as h_1, h_2, h_3, etc. There is more about this in the post about text editor workarounds.

What about data that has been left blank in a list? Sometimes when we have a data set, we have several pieces of information about each unit on the list, but some data has been left blank. There are a couple of things we can do.

Option #1: Change the size of the data set. If the variable is numerical, Option #1 is the only option. In the class survey handed out on Wednesday, for example, we have 38 people who responded to questions in Data Set #1, so n = 38. Three students did not give a response to height in inches, so for that information we have no choice but to change n to 35 for that particular variable. We will need to use n (or N in the case of a population) when calculating the mean and median, as shown below.

Option #2: Create a new categorical value. With categorical variables, we can either ignore the blanks, or create a new category called "left blank" or "did not respond" or "none of the above". For instance, when voting, leaving one field blank on a ballot does not invalidate the entire ballot. You can vote for president, but decide not to vote for anyone for city council, and the presidential vote still counts. There have been ballots made from time to time that gave the option of "none of the above", which is like the idea of "left blank".

Mean, median and mode. There are several ways of stating a single number which gives an idea of the central measure of a set of numbers. The most used numbers are mean, median and mode.

Mean. Also known as average, to take the mean of a set of numbers (and this can only be done with numerical values), find the sum of all the numbers and divide by n. If the data set is a population, the mean is represented by the Greek letter mu, with a subscript of the letter of the variable. If the variable is called x, the mean is mux .If the variable is called d, the mean is mud. If the data set is a sample, we put a bar over the letter used for the variable name, like x-bar or d-bar. (In this text editor, there is no easy way to put a bar above a symbol, so I will type x-bar instead.)

Median. First, the numbers must be put in order, either from low to high or high to low. The median is the number "in the middle", which is to say position (n + 1)/2. If n is odd, then this will mean a specific single position. If n is even, then there are two things "in the middle", and the median will be the average of the two things.

Mode. The mode is the most common value, as long as there are any repeated values. If there are no repeats, there is no mode. If there are repeats and there is a tie for most common, there can be more than one mode.

Let's do some examples.

Data set #1: 11, 11, 9, 7, 13, 12, 8, 5, 12, 11, 4, 4, 8, 8, 5, 2
n = 16
Mean: The sum is 130, so the average is 130/16 = 8.125. The standard for rounding to to round the average to one place farther than the data, so this would round to 8.1

Median: First, put the numbers in order.
13, 12, 12, 11, 11, 11, 9, 8, 8, 8, 7, 5, 5, 4, 4, 2

Because there are 16 things on the list the middle position is (16+1)/2 = 8.5, which is to say we will take the average of the 8th and 9th values. Those two values are the first two 8s on the list, which are in bold and underlined. Obviously, the average of 8 and 8 is 8, so 8 is the median.

Mode: Both 11 and 8 show up on the list three times, which is the most, so both 8 and 11 are modes for this variable.

Data set #2: 33, 32, 35, 25, 24, 22, 20, 21, 19, 18, 17, 17, 16, 15, 9
n = 15

Mean: The sum of the numbers is 323, so the mean is 323/15 = 21.5333..., which rounds to 21.5 if we round to the nearest tenth.

Median: First we put the numbers in order.

35, 33, 32, 25, 23, 22, 20, 21, 19, 18, 17, 17, 16, 15, 9

The middle position is (15+1)/2 = 8, so the value in the eighth position, whether we count left to right or right to left is 21.

Mode: There is only one repeated value on the list, and that is 17.

(Data Set #1: Number of wins of the teams in the AFC at season's end.)
(Data Set #2: Number of wins of the teams in the Eastern Conference of the NBA as of the end of play on Jan. 21, 2009.)

Class notes for 1/14

Today's class was about definitions of terms and symbols.

If a data set includes all members of a particular defined group, that set is called a population.

If the data set is just a subset of a particular defined group, that set is called a sample.

Taking down the information for all members of a particular defined group is called a census.

The members of the data set are called units. If all the units are humans, we called them subjects instead of units.

We can collect several pieces of information about each subject or unit. Each separate piece is called a variable. The legal answers that can be associated with a variable are called values.

Example #1: On the survey, gender is a variable. The legal values are male and female.

Example #2: GPA, listed to the nearest hundredth, is a variable. The legal values are the numbers, 0.00, 0.01, ... 3.99, 4.00, all the numbers from 0.00 to 4.00 counting by hundredths.

The first big split in variable types is between categorical variables, where the values are not numbers, and numerical variables, where the values are numbers. Categorical is sometimes called qualitative data, and numerical is sometimes called quantitative data.

Two types of categorical data: Categorical data can either be ordered or unordered.

Ordered Categorical variables includes things like grades (A, B, C, D, F), class rankings (freshman, sophomore, junior, senior), military ranks and other such data where you can take any two different values and determine which is one is above or below the other.

Unordered Categorical variables do not have a natural ranking associated with them. These include gender, major, left or right handedness, eye color, etc.

There are many types of numerical data. The first split is between discrete and continuous.

The question to ask is this. In a number system, can we talk about the "next highest" or next lowest" number?

If we can define the next highest and next lowest numbers, the numerical variable is discrete. For instance, if an answer must be a whole number, the data is discrete. "How many brothers and sisters do you have?" is answered either 0 or 1 or 2 or so on. You can't answer 2.37.

Things do not have to be integers to be discrete. English wrench sizes get larger by 1/8 of an inch each time you go up a size, so 1/8", 1/4", 3/8", 1/2", 5/8", etc. is a discrete data set.

Things like height and weight are continuous variables. For example, if you get on a scale one Monday and weigh 143 pounds, while the Monday before you weighed 141 pounds, there must be a moment during the week when you weighed 142.728 pounds or 141.3304 pounds. What we tend to do with continuous variables is round them to some set unit, so in that way they read as though they are discrete, though in fact they can take on any value in between the highest and lowest values. Whether that unit is the nearest pound or the nearest half a pound or the nearest tenth of a pound, we have take a continuous variable and made it look like it is discrete.

Syllabus Spring 2009

Math 13: Introduction to Statistics Spring 2009 – Laney College

Instructor: Matthew Hubbard
Text: none
Email: mhubbard@peralta.edu, profhubbard@gmail.com
website: budgetstats.blogspot.com
Office hours: M-W noon to 1 pm in G-201 (math lab) (also available by appointment)
Scientific calculator required (TI-30X IIs or TI-83 recommended)

Important academic schedule dates

Last date to add, if class is not full: Sat., Jan 31
Last date to drop class without a “W”: Sat., Feb. 7
Last date to drop class with a “W”: Sat., April 25

Holidays and professional development days that effect the Mon.-Wed. schedule:

Mon., Jan. 19 Dr. Martin Luther King, Jr. Day
Mon., Feb. 16 President’s Day
Wed. Mar. 25 Professional development day
April 13 through April 18 Spring recess
Mon., May 26 Memorial Day (observed)

Midterm and Finals schedule:

Wed., Feb. 25 Midterm 1
Wed., April 8 Midterm 2
Fri., May 22 Final for 8 am – 10 am class
Fri., May 29 Final for 10 am – noon class

Grading Policy

Homework to be turned in: Assigned every Wednesday, due the next class period
(late homework accepted AT THE BEGINNING of class period after next, 10% off grade)
Quizzes: Wednesdays in weeks without midterms – no make-up quizzes
If arranged at least a week in advance, make-up midterms can be given.

The two lowest scores from homework and the two lowest scores from quizzes will be removed from consideration before grading.

Grading system

Quizzes * 25%
Midterm 1 * 25%
Midterm 2 * 25%
Homework 20%
Final 30%

The lowest grade from Quizzes and the two Midterms will be dropped from the total.
Anyone getting a higher percentage score on the final than the weighted average of all grades combined will get the final percentage instead on the final grade, provided that student has not missed more than two homework assignments.

Academic honesty

Your homework, exams and quizzes must be your own work. Anyone caught cheating on these assignments will be punished, where the punishment can be as severe as failing the class or being put on college wide academic probation.

Class rules

Cell phones and beepers turned off, no headphones or text messaging during class
No food or drink in class, except for sealable bottles. All empty bottles should be put in the recycling bins after class is over.
You will need your own calculator and handout sheets for tests and quizzes. Do not expect to be able to borrow these from someone else.

Student Learning Outcomes

1. Describe numerical and categorical data using statistical terminology and notation.
2. Analyze and explain relationships between variables in a sample or a population.
3. Make inferences about populations based on data obtained from samples.
4. Given a particular statistical or probabilistic context, determine whether or not a particular analytical methodology is appropriate and explain why.

The minimum necessary calculator

There is no assigned text for the class, but it is mandatory that you have a calculator that can do statistics. If you already have a calculator, check with the teacher to see if it can do all the tasks needed for the class. For example, a TI-83 or a TI-84 are very good choices, but if you are going to buy a calculator specifically for this course, you can get one much cheaper. (Note: If you have a TI-89 and you aren't planning to take any math after statistics, you have too much calculator for your purposes, and it might be a good idea to buy a new, cheaper calculator. The TI-89 is designed for people who are going on in math to calculus and beyond, and it makes doing statistics a little harder than it should be.)

I recommend the TI-30XIIs calculator. Texas Instruments does not pay me to say this. The reasons I recommend it are these.

1. It's cheap. The highest price I have seen for it is $19.99 at Walgreen's. I have seen it as low as $13.50 at Radio Shack.

2. It's available at a lot of places. The Laney bookstore should have this calculator, but it is also sold at drug stores like Walgreen's and Long's, electronics stores like Radio Shack and Best Buy, office supply stores like Office Max and Staples and department stores like Target and Wal-Mart. There should be one of these stores somewhere convenient for you.

3. It does a lot of work for you. The TI-83 and TI-84 are a little more useful than the TI-30XIIs, but the price difference is about $100 more. If this is the last math class you will be taking, I can't recommend spending the extra cash for just a few features. (Note: I do NOT recommend the TI-30Xa. It's not quite powerful enough.)

4. It's solar powered. There is also the TI-30XIIb, and the only difference is b is for battery and s is for solar. Spend two bucks more now, save on batteries and help the environment.

5. Even after class is over, it's nice to have a good calculator around the house. Or at least that's my experience.

As I wrote in the syllabus, there is no textbook for the class, but a calculator is mandatory. You will not be allowed to share a calculator with a classmate on quizzes and exams, and you will be expected to know how to use your own calculator. There will be class time alloted to teaching people how to use their calculators, and I would like the class to have as few different types of calculators as possible. I recommend Texas Instrument calculators because I have used most of the models that are useful for a statistics course and should be able to instruct students on their uses. Other brands like H-P or Casio are not be as well known to me, and a student with one of these may be forced to read the instruction manual to find out how to do certain things needed in the course.

Welcome to Math 13 for Spring 2009 at Laney

This blog will be used to update the class notes, keep you informed about the class schedule and other important information. You can ask questions in the comment field on any post, and Prof. Hubbard will see them when he checks his e-mail. Please make sure the comments are about the class itself, as Prof. Hubbard reserves the right to remove any comments that are not regarding statistics.

Again, welcome to the class and I hope you have an enjoyable and informative experience taking Math 13 at Laney.