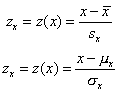Much of statistics deals with data sets. A data set can either be a population, which means it contains everyone in a particular group we are interested in, or it can be a sample, which means a subset of a population. For instance, if everyone in class shows up on the day of a quiz, I could consider that the population of students in the class and the scores on the quiz could be the variable we are collecting. On the other hand, the class could be considered a sample of all students at Laney, or all students at Laney taking statistics, or all students in classes that start at 12:15. The decision on whether it is a sample or a population in many cases can be considered arbitrary, which means that someone made a decision. Arbiter means judge, and some arbitrary decisions are based on simple personal preference while other arbitrary decisions may be based on pre-set rules.

In statistics, there are some symbols that are reserved, which means a particular letter cannot be used to mean just anything. The first two such letters are
N and
n, which mean the size of a population and the size of a sample, respectively. The first kind of data we have dealt with is categorical data, where the answers to the questions are not numerical. How often a particular answer shows up in the population is called the frequency, denoted by
F in a population or
f in a sample. It would be nice if capital letters always meant population and lowercase letters always meant sample, but that is not the case. We also have relative frequency, which is
p in a population and
p-hat in a sample.

Note: the text editor for the blog doesn't allow for fancy marks on letters or even Greek letters, so in some cases when typing, the symbols will have to be replaced with words like
p-hat or
x-bar, which is the way they are pronounced.
There is also the situation of subscripts and superscripts. On the blog, it is possible to show subscripts, like x
3, but if we want to square a number, the text editor doesn't allow making a small number that floats above the line, so instead we will use
x^2. The symbol "^" is also used on your calculator to indicate raising a number to a power.
Frequencies are always whole numbers, either positive integers or zero. Relative frequencies are proportions, numbers between 0 and 1, inclusively. We could write these as fractions, but we often use decimals or percents, which leads to rounding.
Rounding proportionsIn gneral, people like to use percents when talking about proportions because 23% looks like a whole number, though it really isn't. 23% is the same as 23/100 or 0.23. When dealing with large proportions, which is to say proportions over 1%, percent will be the standard. How far we round the number will depend on the sum of all relative frequencies.
For example, if we have four categories and each category has a relative frequency of 1/4, we could write 25% for each. If we add up all relative frequencies and we don't round, the sum will be exactly 1 or 100%.
25%+25%+25%+25= 100%
If instead we have eight categories and each has a relative frequency of 1/8, rounding to the nearest percent gives us 13%. (Without rounding 1/8 = .125, so we would round up.)
13%+13%+13%+13%+13%+13%+13%+13%=104%
If the sum is more than one tenth of one percent away from 100%, we need to round to more places. In this case 1/8 = 12.5% exactly so if we write the proportions to the nearest tenth of a percent, we get
12.5%+12.5%+12.5%+12.5%+12.5%+12.5%+12.5%+12.5%=100%
With 1/3 = .333......, we don't get so lucky.
33%+33%+33%=99% (Close, but not 100%.)
33.3%+33.3%+33.3%=99.9% (Still not exactly right.)
33.33%+33.33%+33.33%=99.99% (Still not exactly right, and it never will be.)
Since in some cases, rounding will always produce some error, we make the arbitrary decision that being within one tenth of one percent is close enough, which means between 99.9% and 100.1%, inclusive. So with in this case, we should round to the nearest tenth of a percent.
Scales based on powers of 10: The most famous scale base on powers of ten in percentage, which really means "per 100". It is much more common to see "53% of the people agree with the president's plan" than ".53 of the people..." or "53 out of every 100 people...". Technically, all those phrases are saying the same thing, but percentage is the most popular.
One of the places where decimals are used for proportions is in the sports pages. A batting average in baseball (hits/at bats) is given as a percent to three decimal place, and likewise winning proportions (win/total games) are written as .
xxx. If a batter has 27 hits in 92 at-bats, the batting average 27/92 = .293478261... is shortened to .293 and pronounced "two ninety three". Likewise, a team who has won 17 games and lost 5 will have a winning proportion of 17/22 = .77272727... = .773, and often stated as "team has a winning percentage of seven seventy three." Technically, this is a mistake, because "percentage" means out or 100. The correct word from the dictionary, which no one ever uses, is "permillage", which means out of 1,000. The team in question would have a winning percentage of 77/100, and a winning permillage of 773/1000.
In both of the cases from the sports pages, the greater number of place after the decimal is used to break ties. For example, a team with 14 wins and 4 losses is at .778, which is better than 17 wins and 5 losses, while 20 wins and 6 losses is at .769, so is slightly worse.
To get a number based on a power of 10 scale, you take the proportion and multiply by the power of ten, so it is either
p*scale or
p-hat*
scale, depending on population or sample. Besides greater precision for breaking ties, sometimes we need greater precision because the proportions are so small.
When I ask a class what is the legal limit for blood alcohol while driving, invariably someone will say "point oh eight" and most people will agree. But .08 is wrong. .08 = 8%, and the correct answer is .08% = .0008. I don't blame the students. The number is badly represented and it is an easy mistake to make. Let's take a look at the number on other scales of 10.
.08 out of 100 is the same as
.8 out of 1,000 0r
8 out of 10,000 or
80 out of 100,000
80 parts out of 100,000 is a tiny proportion. To give an idea, ounce of pure alcohol mixed into ten gallons of blood would give you 78 parts out of 100,000, and most people have between a half gallon and a gallon and a half of blood in their body, between 4 and 12 pints. The amount of alcohol in a person's blood stream that is over the legal limit is about the same amount of alcohol as found in a capful of mouthwash used after brushing your teeth.
We will be dealing with much smaller proportions later in the class, where there are things that can be hazardous to your health at ranges measure in parts per billion, but for now, we will look at the per 100,000 scale for another type of statistic, measurements of mortality rates.
Here are the number of homicides in some local cities in 2007.
Oakland: 124 homicides
Richmond: 28 homicides
San Francisco: 98 homicides
Clearly, comparing these numbers is misleading, because we know these cities have very different numbers of citizens, so the standard way to measure these statistics is the per 100,000 population scale, which we find by the formula
f/
n*
scalewhich in this case is
(# of homicides)/(city population) * 100,000
Oakland's population in 2007 is estimated at 415,000, Richmond at 106,000 and San Francisco at 825,000, so the murder rates on this standard scale are as follows
Oakland: 124/415000 * 100000 = 29.9
Richmond: 28/106000 * 100000 = 26.4
San Francisco: 98/825000 * 100000 = 11.9
So even though more people were murdered in San Francisco than in Richmond in 2007, the murder rate in Richmond was over twice as high, because Richmond has barely 1/8 of the population of San Francisco. (note: The trends for the three cities this decade are going in different directions. Oakland's murder rate is on the rise, while Richmond's is falling and San Francisco's has stayed about the same.)
Calculating proportions (probabilities): There are times when we will need to find new proportions from information previously calculated, either adding and subtracting old numbers or multiplying or dividing. It's best to use the fractional forms of the data when available, then round the answers after using the exact numbers instead of using answers that might have been rounded. Every time you use a rounded answer in a calculation, there is a change to increase the rounding error even more.