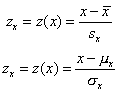
The idea behind z-scores is that we can compare data from completely different numerical data sets by changing the scale to be the distance away from the average, with the new yardstick being the standard deviation. We can take z-scores and the first two pages of the notes to see how common a particular z-score is.
Example: let mux = 63.6 and sigmax = 2.5, which are the average and standard deviation for heights in inches of females.
1) What is the z-score for 67 inches? What percentage of the female population is greater than 67 inches tall?
2) What is the z-score for 64 inches? What percentage of the female population is less than 64 inches tall?

Going the other direction, we have the third page of the notes, which gives z-scores to three decimals that correspond to percentiles in the population. To find the raw score that corresponds to that percentile, use the formulas shown at the left.
3) To the nearest tenth of an inch, what is the height that corresponds to the 96th percentile in U.S. women's heights?
4) To the nearest tenth of an inch, what is the height that corresponds to the 24th percentile in U.S. women's heights?
Answer in the comments.


2 comments:
I agree with all of these steps. I did come up with a different Z score for 67, which came out to 1.36. Looking at the possitive Z values this came out to .9131, or 91.31% of women are 67 inches or shorter. So 8.7% of women are 67 inches or taller.
Answers corrected. Thanks, Benjamin.
Example: let mu_x = 63.6 and sigma_x = 2.5, which are the average and standard deviation for heights in inches of females.
1) What is the z-score for 67 inches? What percentage of the female population is greater than 67 inches tall?
z(67) = (67-63.6)/2.5 = 1.36
1.36 corresponds to .9131, but that means 91.31% of women are 67 inches tall or less. 100-91.31 = 8.69, so 8.69% are 67 inches tall or more.
2) What is the z-score for 64 inches? What percentage of the female population is less than 64 inches tall?
z(67) = (64-63.6)/2.5 = .16
.16 corresponds to .5636, and that means 56.36% of women are 64 inches tall or less.
3) To the nearest tenth of an inch, what is the height that corresponds to the 96th percentile in U.S. women's heights?
The 96th percentile z-score is 1.751.
63.6+1.751*2.5 = 67.9775, which when rounded to the nearest tenth of an inch is 68.0 inches.
4) To the nearest tenth of an inch, what is the height that corresponds to the 24th percentile in U.S. women's heights?
The 24th percentile z-score is -0.706.
63.6-0.706*2.5 = 61.835, which when rounded to the nearest tenth of an inch is 61.8 inches.
Post a Comment